정확하게 말하면 규제화(regularization)는 일부 미지수의 값을 아주 작게 만들어 그 영향을 줄임으로써 마치 미지수의 개수가 적어진 효과를 가져온다. 가중치 값이 커지는 것을 막는다는 제한, 규제의 의미가 있데 이런 규제화의 종류에는 L1 norm(노름)과 L2 norm이 존재한다. 각 각의 설명을 위해 두 종류를 비교해 보도록 하겠다. 다음의 표에 기재된 수식을 한번 보자.

먼저 λ (람다)는 규제화의 세기를 조절하는 변수이며 의 값을 크게 주면 강한 규제를, 값을 작게 주면 약한 규제를 줄 수 있다. 수식을 보면 입력 feature가 d개가 있을 때 바이어스(b)를 w0으로 표현해 총 d+1개의 w가 있고 L1, L2 모두 w 앞에 를 곱해 가중치의 크기를 규제하는 형태의 수식이다. 차이가 있다면 w 의 부호를 상쇄시켜 절대적인 크기를 얻고자 사용한 방법에 있다. L1은 w 에 절댓값을 취했고 L2는 w 의 제곱을 해주었는데 이 차이가 어떠한 결과를 가져왔는지 다음의 예시를 통해 알아보자.
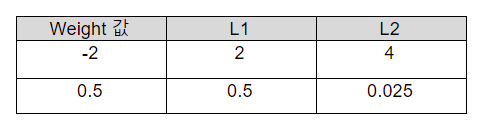
L2는 제곱의 특성상 가중치 값이 1보다 크면 강하게 규제가 되고 1보다 작으면 약하게 규제가 되는 것을 확인할 수 있다. 또한 0.1 -> 0.01 -> 0.0001 … 이 되기 때문에 규제를 하면서도 0을 만들지 않으면서 결과에 큰 영향을 주지 않는 작은 수들로 만드는 특징이 있다. 그에 반해 L2는 가중치 값을 에 의해 똑같이 줄이는데 결국 규제를 계속하다 보면 가중치들을 하나씩 0으로 만들어 완전히 제외시키는 특징이 있다. 그래서 feature의 수가 많고 그 중 일부분만 중요하다면 L2를 사용하는 것이 적절하다. L1은 feature간의 규제가 L2 보다 강하게 들어가며 심하면 feature들이 모두 0이 될 수 있어 보통 L2를 많이 사용한다.
여기까지 규제화에 대해서 살펴보았다. 규제화는 구현이 쉽고 오버피팅을 방지하는데 어느 정도 성능을 가지고 있다. 그러나 신경망이 복잡 해진다면 사실 가중치를 감소시키는 방법으로는 부족하다. 이를 위해 등장한 기법이 드롭아웃(Drop-out)이다.
작성자 홍다혜 ghdek11@gmail.com / 이원재 wonway333@gmail.com
'【1】Deep Learning 시작하기 > 규제화라는 게 있다' 카테고리의 다른 글
| Drop-out (0) | 2020.01.19 |
|---|---|
| Overfitting 해결하기 (0) | 2020.01.17 |
| Overfitting이 무엇일까? (0) | 2020.01.16 |


