스트라이드는 사전적으로 ‘보폭’이라는 의미를 갖는다. 마찬가지로 입력데이터에 필터를 적용할때를 생각해보자. 아래의 예제는 앞에서 계속 다루었던 (4,4)사이즈의 입력 데이터에 (3,3) 필터를 적용한 예이다.
여기에 우리가 배운 세임 패딩을 적용한다면 다음과 같이 나타낼 수 있다.

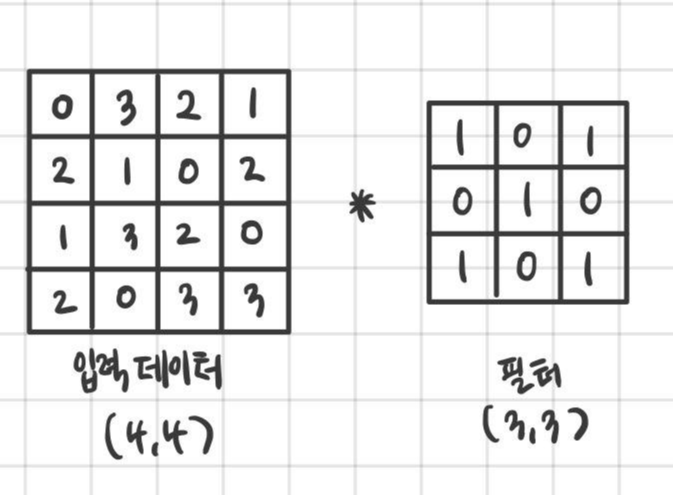
패딩을 적용한 입력 데이터에 합성곱 연산을 하면 아래의 그림처럼 진행 될 것이다.

그림에서 필터가 적용되는 보폭을 보자. 지금까지는 보았던 연산들이 그러하듯 왼쪽 위부터 오른쪽 방향으로 한칸씩 전진하며 합성곱 연산이 적용된다. 즉 앞에서 본 예시는 모두 스트라이드가 1이다. 만약 스트라이드가 3이라면 세칸씩 이동하면서 필터를 적용한다. 이를 그림으로 나타내면 다음과 같다.
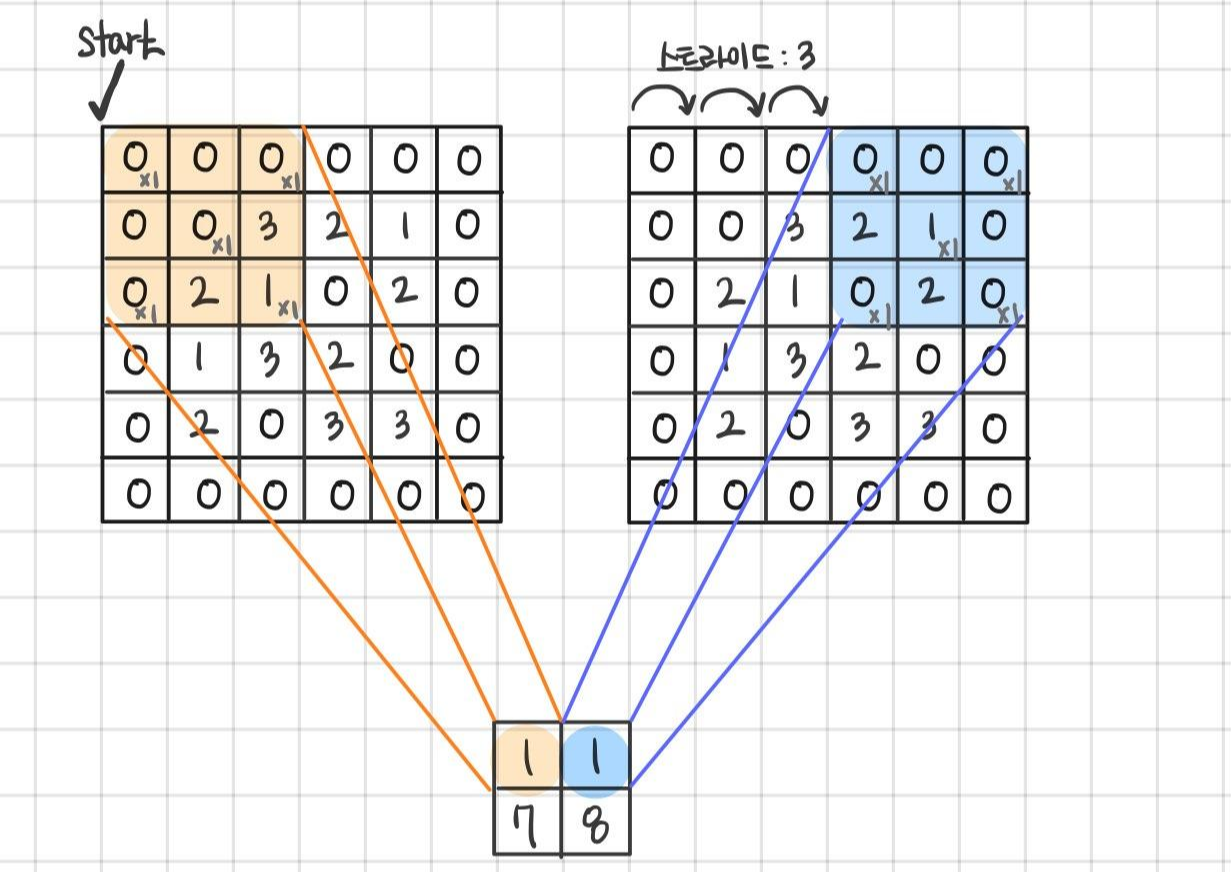
스트라이드를 1에서 3으로 조정했더니 연산의 출력 데이터 크기가 달라진 것을 확인 할 수 있다. 스트라이드가 작으면 출력의 사이즈가 커지고 반대로 커지면 출력 사이즈는 작아진다.
그렇다면 패딩의 폭과 출력 사이즈의 관계는 어떠할까? 패딩의 사이즈 즉, 폭이 두꺼워지면 입력 데이터의 크기가 커지므로 출력 사이즈 또한 증가하게 된다. 이렇게 출력의 크기는 입력 데이터, 패딩, 스트라이드의 크기에 모두 영향을 받는다. 입력데이터 (Hi,Wi), 필터 (F, F), 패딩 폭 P, 스트라이드 S 일때 출력데이터의 크기 (Ho,Wo)는 다음의 공식으로 구할 수 있다.

※ 단 정수로 나눠떨어지는 값이어야 한다.
[도전! 연습문제_1]
입력데이터 (10, 10), 필터 (3, 3), 패딩 폭 P = 2, 스트라이드 S=1 일때 출력데이터 (Ho,Wo)의 크기를 구하여라.
풀이)
입력데이터 Hi=10, Wi=10 이고 필터 F=3, 패딩 폭 P=2 , 스트라이드 S=1일때
출력데이터의 크기 (Ho,Wo)는
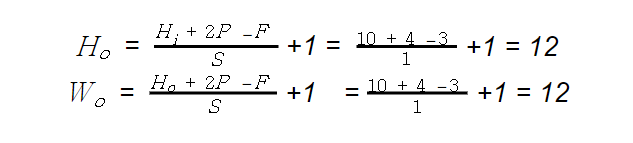
∴ 출력데이터의 크기(12, 12)
참고) 필터의 사이즈가(3, 3)이고 패딩의 폭이 2인것으로 보아 풀 패딩이 적용되었다.
[도전! 연습문제_2]
입력데이터 (13, 17), 필터 (5, 5), 패딩 폭 P = 2, 스트라이드 S=2 일때 출력데이터 (Ho,Wo)의 크기를 구하여라.
풀이)
입력데이터 Hi=13,Wi=17 이고 필터 F=5, 패딩 폭 P=2 , 스트라이드 S=2일때
출력데이터의 크기 (Ho,Wo)는

∴ 출력데이터의 크기(7, 9)
참고) 필터의 사이즈가(5, 5)이고 패딩의 폭이 2인것으로 보아 세임 패딩이 적용되었다.
여기까지 입력데이터, 필터, 패딩, 스트라이드에 대해 알아보았다. 이제 여러분은 합성곱 연산의 작동 원리와 그 결과로 얻게되는 피처맵의 크기까지 계산 할 수 있다. 지금까지 다룬 과정들은 ‘합성곱 층’이라는 CNN의 핵심적인 계층에서 일어난다.

CNN의 또 다른 구성 요소로 ‘풀링 층’이 있다. 사실 엄밀히 말하면 합성곱 층에서 최종적으로 얻은 피처맵은 렐루(ReLU) 활성화 함수를 적용해 값을 산출하여 풀링층으로 전달한다. 기존에 다루었던 신경망을 생각해보자. 한층의 노드들은 다음층의 입력으로 들어가기 전에 활성화 함수를 통과했었다. CNN에서도 마찬가지로 합성곱 층에서 풀링층으로 넘어가는 단계에 활성 함수를 적용하며 이때 활성 함수로는 속도와 정확성이 좋은 렐루가 사용된다.
다시 본론으로 돌아와 풀링 층을 말하자면 풀링층은 피처맵의 크기를 작게만들어 신경망의 계산량을 줄이는 기법이다. 합성곱 층의 출력으로 나온 피처맵이 풀링 층의 입력으로 들어가면 크기가 작아져서 반환된다.

위 그림은 높이와 너비가 4, 채널 수가 3인 피처 맵이 입력으로 들어와 높이와 너비가 2로 줄어든 풀링이 된 그림이다. 풀링 연산은 채널마다 독립적으로 작동하므로 채널의 수가 변하지 않는다. 풀링은 입력 데이터의 영역별로 하나의 원소를 뽑는다. 뽑는 기준은 최대값, 최소값, 평균 값이 있으며 이를 순서대로 최대 풀링(Max pooling), 최소 풀링(Min pooling), 평균 풀링(Average pooling)이라고 한다.
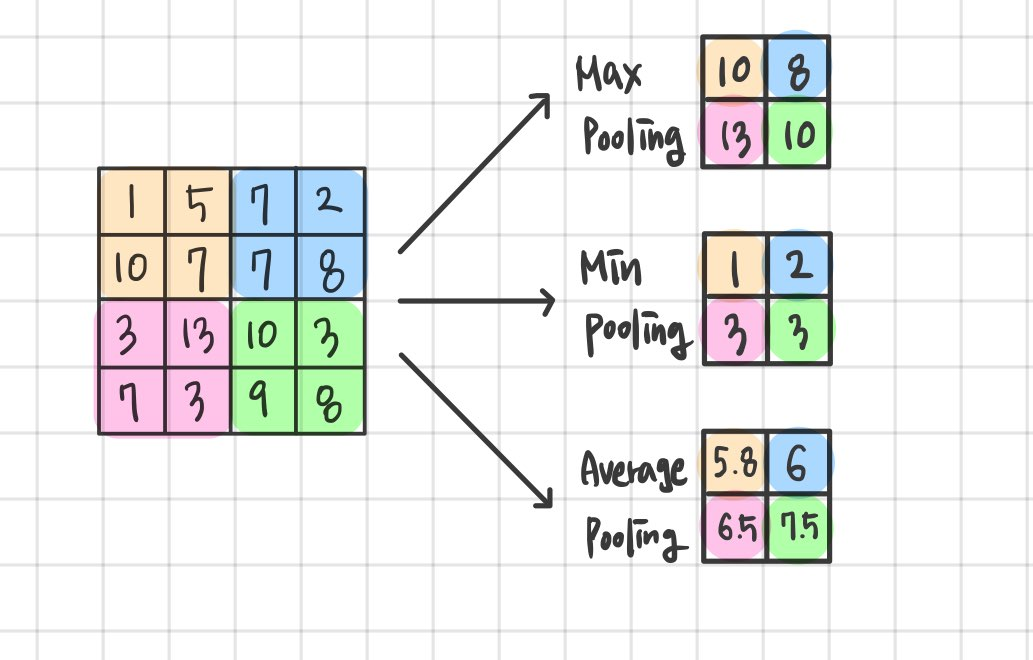
위 그림은 (4,4)크기의 피처맵을 (2,2)크기의 영역으로 나누어 최대 풀링, 최소 풀링, 평균 풀링 모습이다. 이때 (2,2) 크기의 영역을 풀 크기라고 하며 풀링에서는 풀 크기와 스트라이드를 같은 값으로 설정하여 겹치지 않게 한다. 예시에서는 풀 크기가 (2,2) 이므로 스트라이드는 2가 되며 이는 실제로 가장 많이 쓰이는 설정이다. 최대 풀링은 영역별로 가장 중요한 특징을 추출하는 반면, 평균 풀링은 영역의 모든 값들을 고려하여 평균 값을 내므로 매우 부드러운 특징을 추출한다. 그러므로 최대 풀링이 가장자리(edge)나 질감(texture)와 같은 이미지의 구조를 포착하는데 유용하므로 이미지 인식 분야에서 많이 사용되어진다. 여기까지 합성곱층과 풀링층을 다루었다. 한 묶음 처럼 여겨지는 이 두 계층은 원본 이미지의 특징을 찾는 과정이므로 여러번 반복되어서 사용 된다.
마지막으로 다룰 CNN의 구성요소는 ‘완전 연결 계층’이다. 완전 연결 계층은 우리가 1장에서 다루었던 신경망에서 등장한 계층으로 한 노드가 이전 층의 모든 노드와 연결 되어있는 구조이다. 우리에게 매우 익숙한 아래의 그림을 보자. 완전 연결 계층으로 구성된 신경망이다.

입력데이터가 합성곱 층을과 풀링층을 통과한 후에 바로 이 완전 연결 계층으로 넘어간다. 풀링층의 출력으로 얻은 피처맵을 수직으로 펼쳐서 완전 연결 계층의 입력으로 넣어준다. 완전 연결 계층에서는 합성곱층에서 찾은 원본 이미지의 특성들을 이용해 분류의 과정을 거친다. 완전 연결 계층의 출력층에서는 다중 출력에 사용되는 활성함수인 소프트맥스(softmax)를 사용해 최종 출력을 만든다.
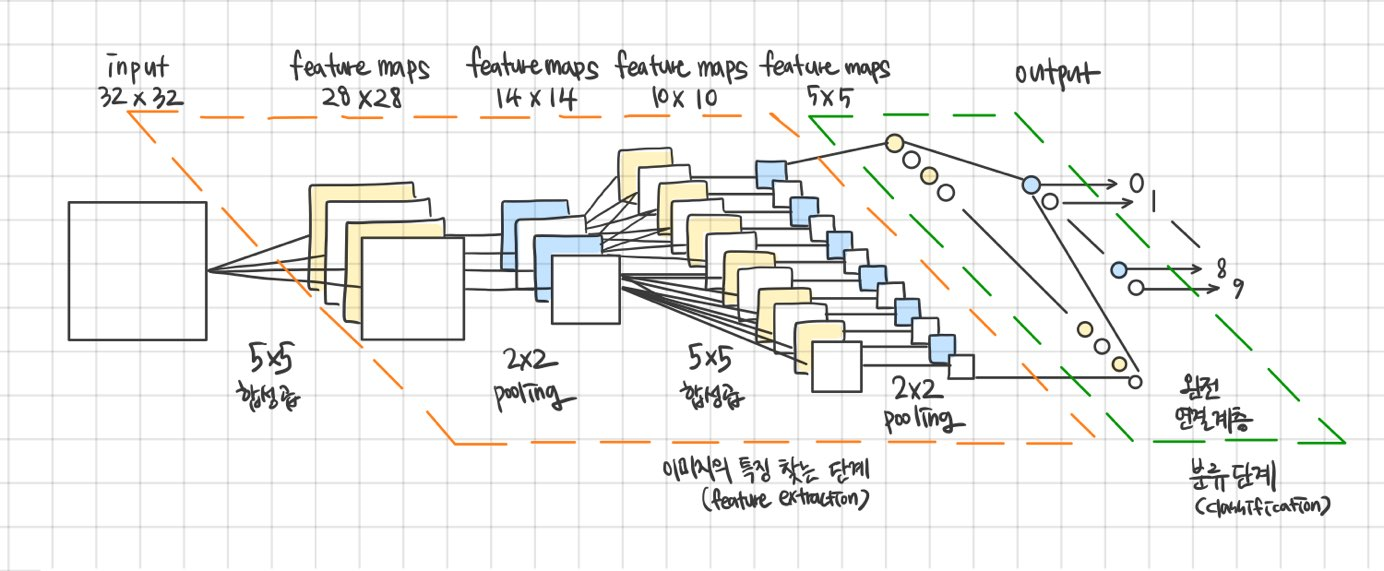
자 아래에 CNN의 과정들이 한 눈에 정리가 될 수 있는 그림이 있다. 원본 이미지가 CNN의 입력으로 들어갔을 때 출력을 반환하기 까지 눈으로 그림을 따라가보자. 중간에 이해의 흐름이 끊긴다면 그 부분의 설명을 다시 보고 내려오는 것을 추천한다. 이 흐름을 이해한다면 코드의 구현또한 문제 없을 것이다!
작성자 홍다혜 ghdek11@gmail.com / 이원재 ondslee0808@gmail.com
'【2】CNN_합성곱 신경망 > Convolutional Neural Networks의 이해' 카테고리의 다른 글
| 선생님, Padding은 뭔가요? 밸리드 패딩 / 풀 패딩 / 세임 패딩 (0) | 2020.02.05 |
|---|---|
| 곱셈과 덧셈만 알면 정말 쉬운 ‘합성곱' (2) | 2020.02.04 |
| 합성곱 신경망(CNN) / 고양이의 눈에서 답을 얻다. (0) | 2020.02.03 |


